문제 요약

내 코드와 설명
- 입력한 숫자를 목록에 저장하고 인덱스 1부터 for 문까지 각 숫자를 찾습니다.
이전 숫자보다 크거나 같으면 big_cnt에 1을 더합니다. 이때 big_cnt 값이 ans보다 크면 ans는 big_cnt로 업데이트된다. 이전 숫자보다 크거나 같지 않으면 big_cnt를 1로 초기화합니다.
이번에는 숫자가 이전 숫자보다 작거나 같은지 확인하기 위해 새로운 if 문이 실행됩니다. 연산 방식은 크거나 같은지 확인하는 if 문과 동일합니다.
이때 ans 변수에 접근하여 small_cnt의 값을 갱신하는데, 이는 연속된 크거나 같은 숫자의 개수와 연속된 작거나 같은 숫자의 최대값을 ans에 저장하게 되며, ans만 있다면 출력은 문제를 해결할 수 있습니다
n = int(input())
num_list = list(map(int, input().split()))
ans = 1
big_cnt = 1
small_cnt = 1
for i in range(1, len(num_list)):
#커지는 수
if num_list(i) >= num_list(i-1):
big_cnt+=1
if ans < big_cnt:
ans = big_cnt
else:
big_cnt = 1
#작아지는 수
if num_list(i) <= num_list(i-1):
small_cnt+=1
if ans < small_cnt:
ans = small_cnt
else:
small_cnt = 1
print(ans)기타 코드 및 설명 – 동적 프로그래밍(DP)
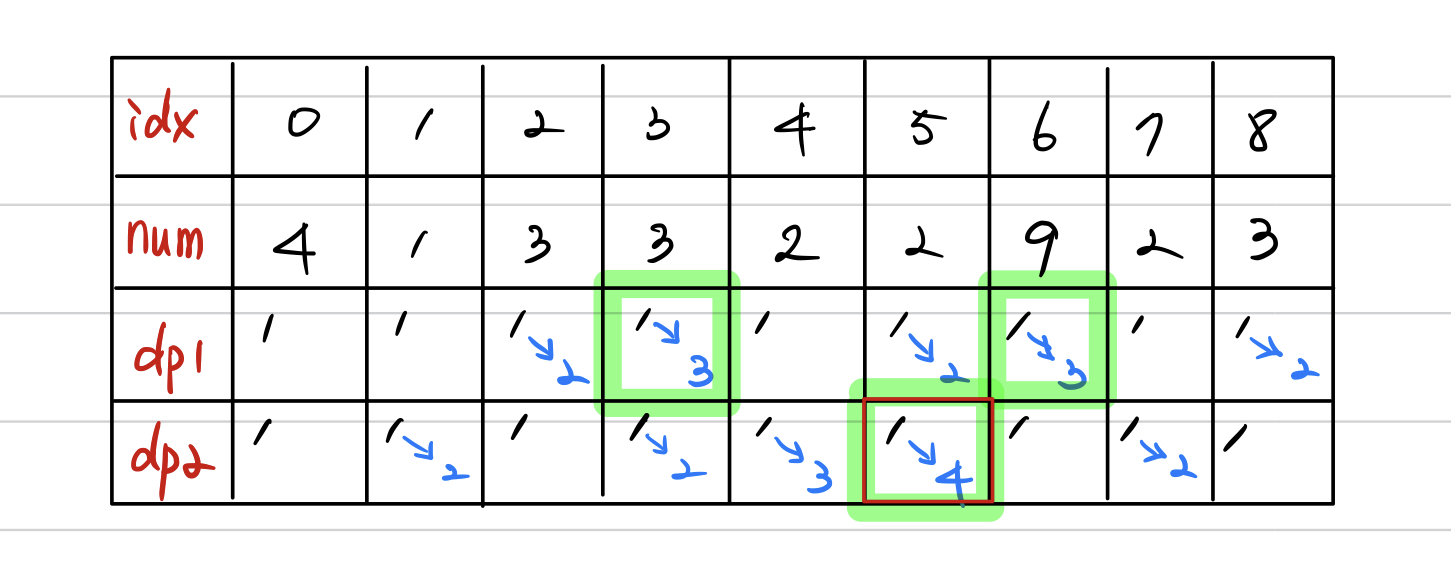
- dp1: 연속적으로 증가하는 숫자를 저장
dp2: 연속적으로 감소하는 숫자를 저장
n = int(input())
num_list = list(map(int, input().split()))
dp1 = (1 for _ in range(n)) #가장 긴 증가하는 수열
dp2 = (1 for _ in range(n)) #가장 긴 감소하는 수열
for i in range(1, n):
if num_list(i-1) <= num_list(i):
dp1(i) = dp1(i-1) + 1
if num_list(i-1) >= num_list(i):
dp2(i) = dp2(i-1) + 1
print(max(max(dp1), max(dp2)))
답장 메시지
다이나믹 프로그래밍이 통달하지 않았기 때문에 문제점을 보고 간단한 구현 방법을 생각했습니다. 동적계획법 이론에서와 마찬가지로 하위 문제를 풀고 결과를 필요할 때 재사용하여 동적계획법 이론을 다시 살펴보고 적용하는 것은 좋은 경험이었습니다. 앞으로 더 잘해보자.